Re-initialization Free Level Set Evolution
via Reaction Diffusion
[Paper] [Supplementary] [MATLAB
CODE]
Kaihua Zhang, Lei Zhang , Huihui
Song and David Zhang
Dept. of Computing, The Hong Kong
Polytechnic University, Hong Kong, China

(a) Basic flow diagram of traditional level set
evolution.
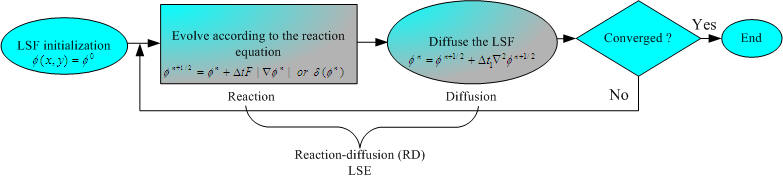
(b) Flow diagram of our proposed RD level set
evolution.
Abstract ¡ª This paper
presents a novel reaction-diffusion (RD) method for implicit active contours,
which is completely free of the costly re-initialization procedure in level set
evolution (LSE). A diffusion term is introduced into LSE, resulting in a RD-LSE
equation, to which a piecewise constant solution can be derived. In order to
have a stable numerical solution of the RD based LSE, we propose a two-step
splitting method (TSSM) to iteratively solve the RD-LSE equation: first
iterating the LSE equation, and then solving the diffusion equation. The second
step regularizes the level set function obtained in the first step to ensure
stability, and thus the complex and costly re-initialization procedure is
completely eliminated from LSE. By successfully applying diffusion to LSE, the
RD-LSE model is stable by means of the simple finite difference method, which
is very easy to implement. The proposed RD method can be generalized to solve
the LSE for both variational level set method and PDE-based level set method.
The RD-LSE method shows very good performance on boundary anti-leakage, and it
can be readily extended to high dimensional level set method. The extensive and
promising experimental results on synthetic and real images validate the
effectiveness of the proposed RD-LSE approach.
¡¡
1.
Motion of dumbbell driven by mean curvature
¡¡
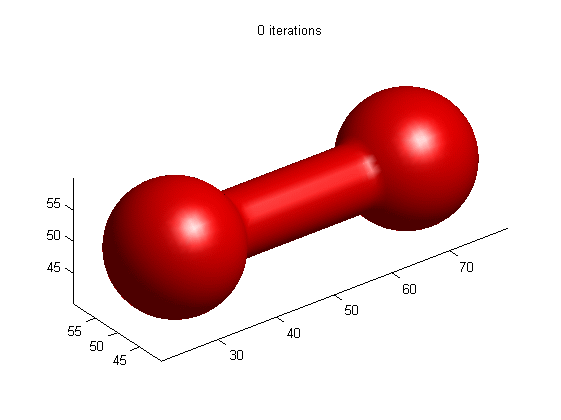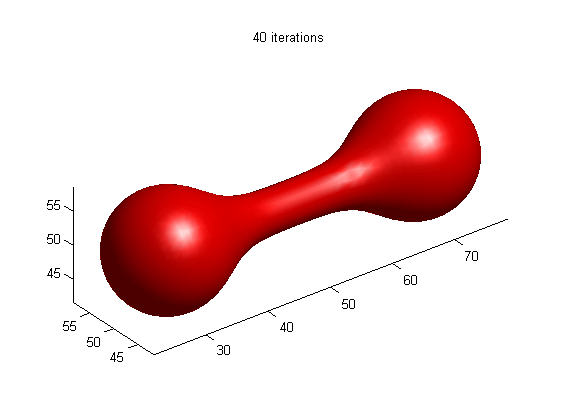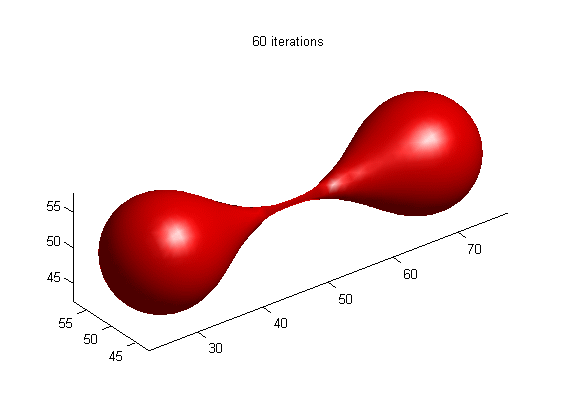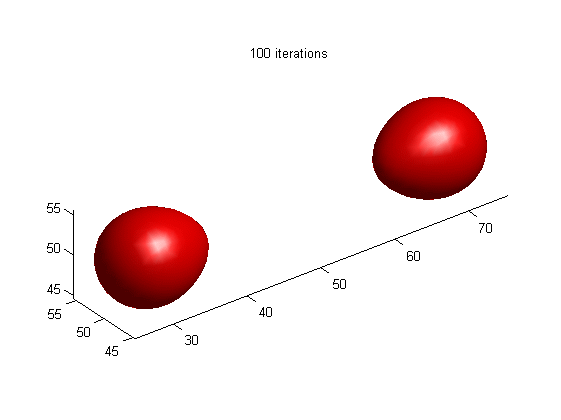
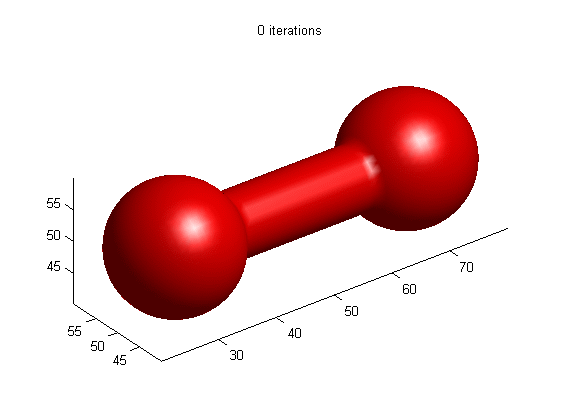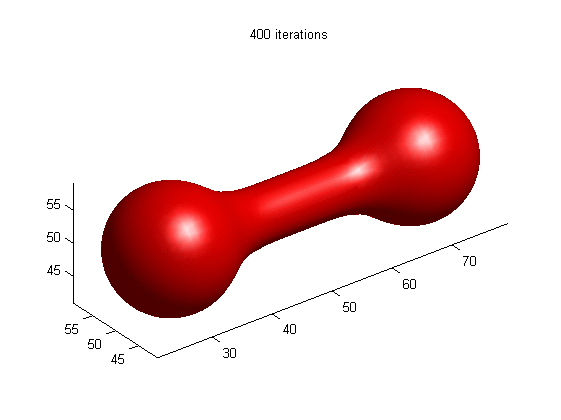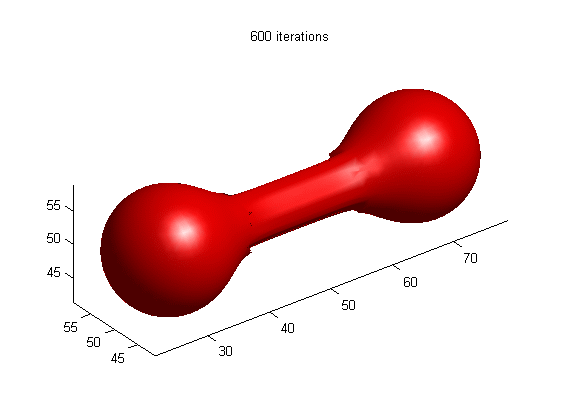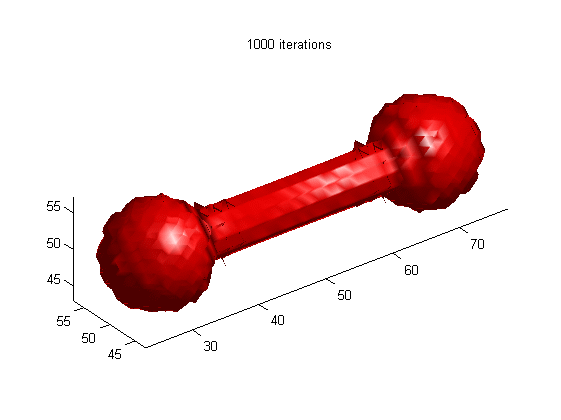
(a) LSE by RD
[1]
(b) LSE without re-initialization
¡¡
¡¡
2. GAC
model [7] implemented by RD method on an image with interior boundary.
¡¡
¡¡
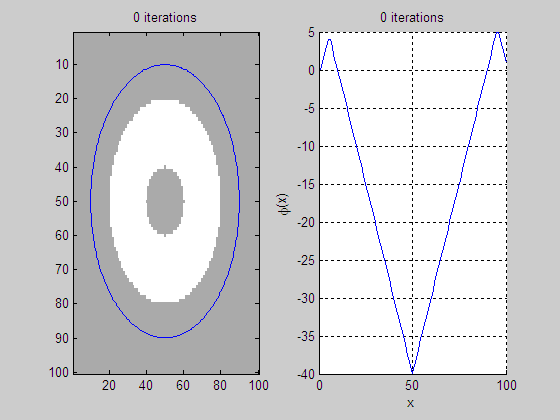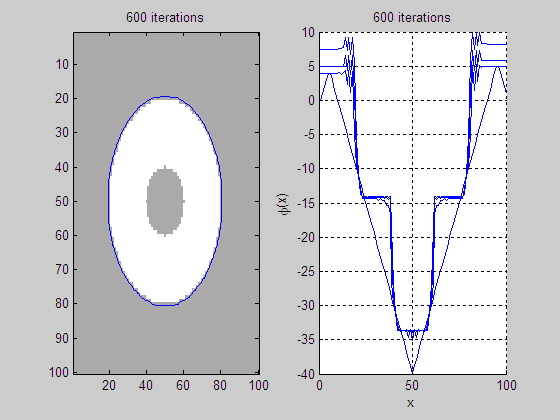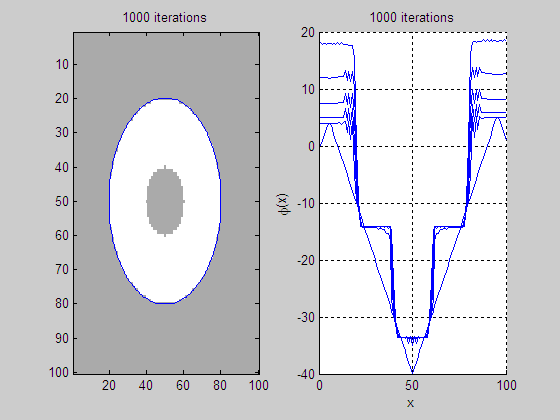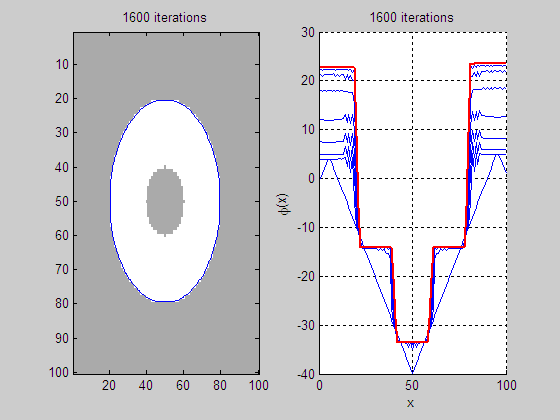
(a)
Level set evolution (LSE) (b)
Evolution of middle slice of LSF
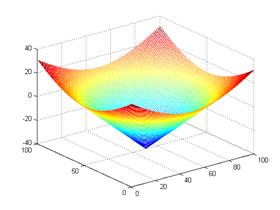
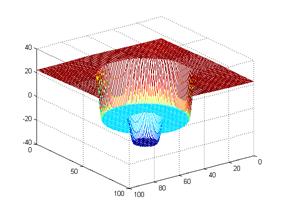
(c)
Initial level set function
(LSF)
(d) Final LSF
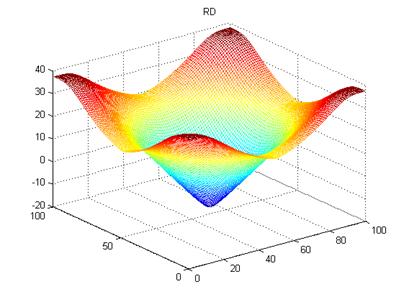
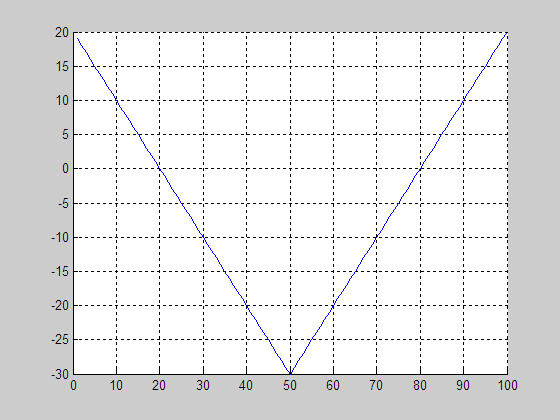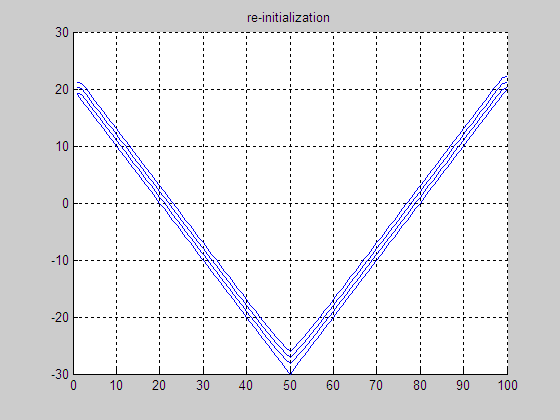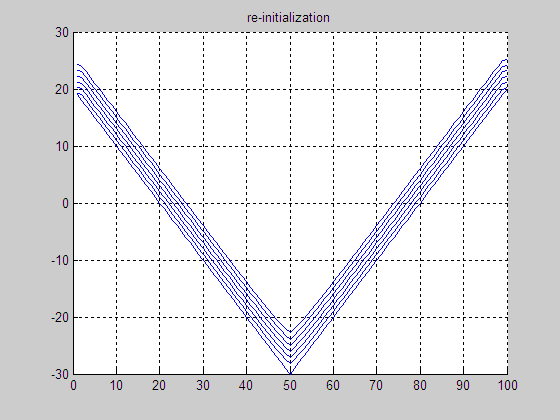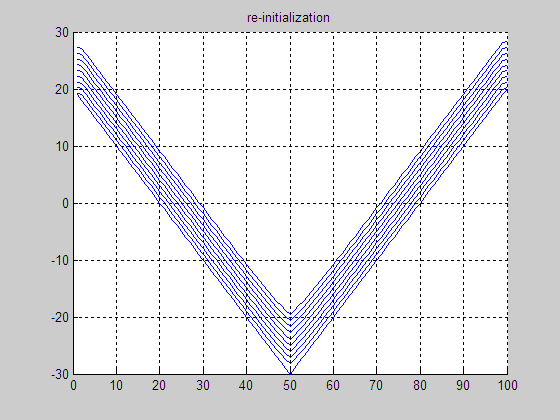
3. LSE
of PDE-based level set driven by constant force
¡¡
¡¡
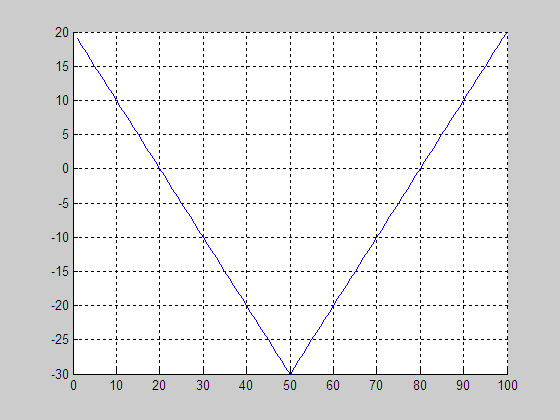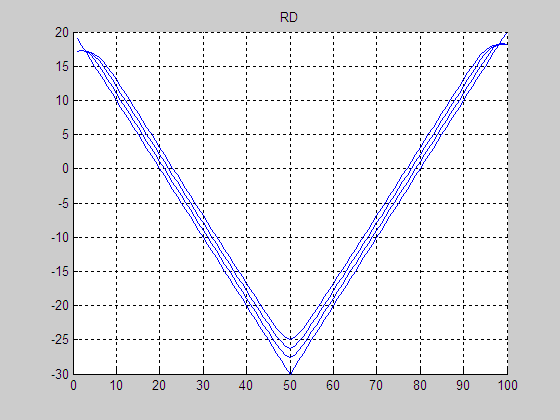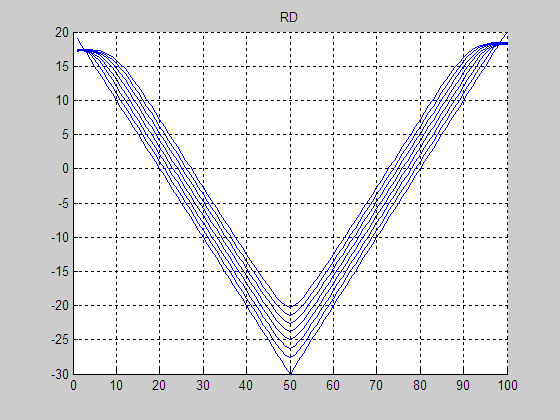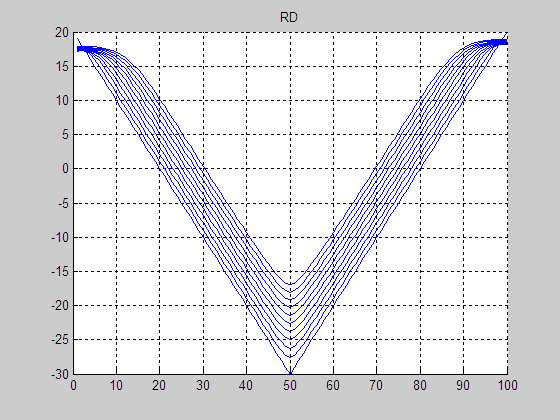
(a) Result by RD
[1]
(b) Final LSF by RD [1]
(c) Result by
re-initialization
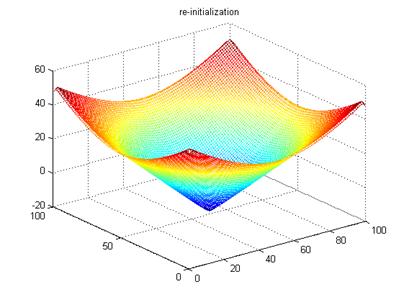
(d) Final LSF by re-initialization
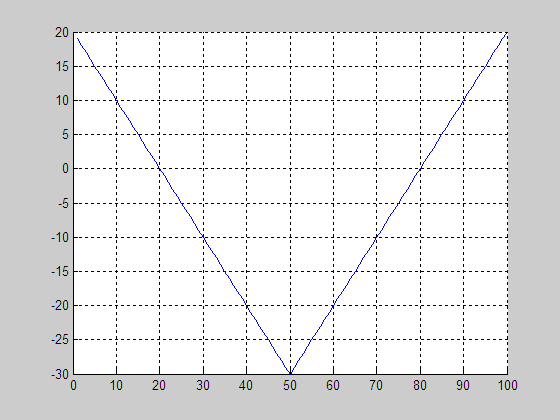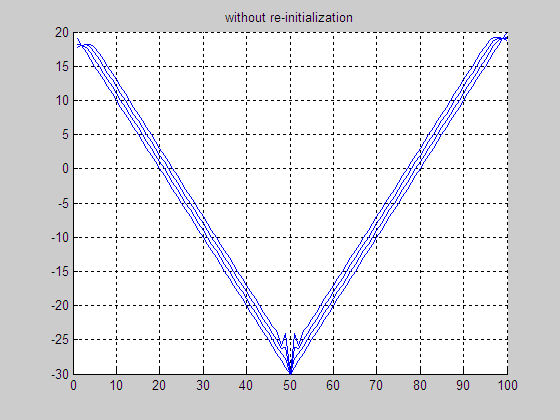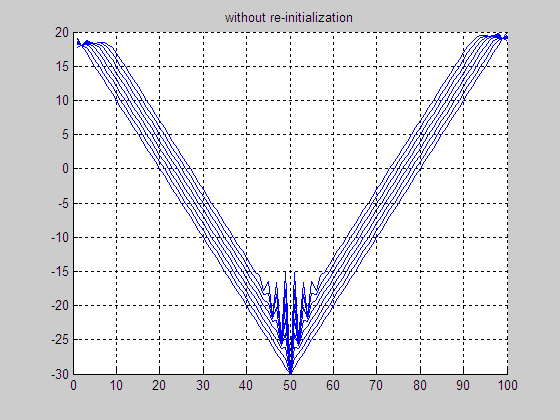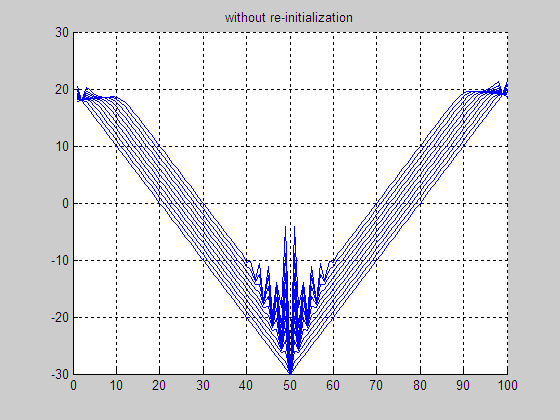
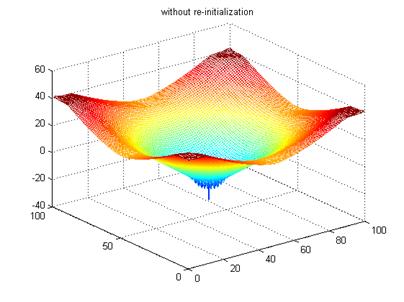
(e) Result without
re-initialization
(f) Final LSF without re-initialization
¡¡
References:
[1] K.Zhang, L.Zhang, H.Song, and D.Zhang, ¡°Re-initialization
Free Level Set Evolution via Reaction Diffusion,¡± IEEE Trans. on Image
Processing, to appear.
Our
former related work
[2] K.Zhang,
L.Zhang, H.Song and W. Zhou, ¡°Active contours with selective local or global
segmentation: a new formulation and level set method,¡± Image and Vision
Computing, vol. 28, issue 4, pp. 668-676, April 2010.Paper Source code Website
[3] K.Zhang, H.Song, and
L.Zhang, ¡°Active contours driven by local image fitting energy,¡± Pattern
recognition, vol.43, no.4, pp.1199-1206, 2010.Paper Source code
[4] K.Zhang, L.Zhang and S.Zhang, ¡°A VARIATIONAL
MULTIPHASE LEVEL SET APPROACH TO SIMULTANEOUS SEGMENTATION AND BIAS
CORRECTION,¡± ICIP 2010.Paper Source code
Other
related work
[5] C.
Li, C. Xu, C. Gui, and M. D. Fox, ¡°Level set evolution without
re-initialization: A new variational formulation,¡± Proc. IEEE Conf. Computer
Vision and Pattern Recognition, vol. 1, pp. 430¨C436, 2005.
[6] X.Xie, ¡°Active Contouring Based on Gradient Vector
Interaction and Constrained Level Set Diffusion,¡± IEEE Trans. Image
Processing, vol. 19, no. 1, pp. 154-164, 2010.
[7] V.Caselles, R.Kimmel, and G.Sapiro, ¡°Geodesic Active
Contours,¡± Int. J. Comput. Vis., vol.22, no.1 pp. 61¨C79,1997.
[8] T. Chan and L. Vese, ¡°Active contours without edges,¡± IEEE
Trans. Image Process, vol. 10, no. 2, pp. 266¨C277, Feb. 2001.
[9] C. Li,
C. Kao, J. Gore, and Z. Ding, ¡°Implicit Active Contours Driven by Local Binary
Fitting Energy,¡± Proc. IEEE Conf. Computer Vision and Pattern
Recognition, pp. 1¨C7, 2007.
[10]C. Li,
C. Xu, C. Gui, and M. D. Fox, ¡°Distance Regularized Level Set Evolution and Its
Application to Image Segmentation,¡± IEEE Trans. Image Processing, vol.
19, no. 12, pp. 154-164, Dec. 2010.