 Lei Zhang¡¯s homepage
Lei Zhang¡¯s homepage
Experimental results of the manuscript:
¡°Image Deblurring and Super-resolution by Adaptive Sparse Domain Selection and Adaptive Regularization¡±
By Weisheng Dong, Lei
Zhang, Guangming Shi, and Xiaolin Wu
to appear, IEEE Trans. on Image Processing.
Paper:
download here
Matlab Code: download here
Part A: Results on Image Deblurring
Notes:
(1)
The
deblurring method in [1] is labeled as ¡°Surrogate¡±;
(2)
The
deblurring method in [2] is labeled as ¡°FISTA¡±;
(3)
The
deblurring method in [5] is labeled as ¡°SWTV¡±;
(4)
The
deblurring method in [6] is labeled as ¡°L0Spar¡±;
(5)
The
deblurring method in [8] is labeled as ¡°BM3D¡±;
(6)
The
proposed method by using only ASDS is
labeled as ASDS, by using ASDS plus AR
regularization is labeled as
ASDS-AR, by using ASDS with both AR and non-local regularization is
labeled as ASDS-AR-NL.
(7)
The
proposed deblurring method with training image dataset 1 or dataset 2 is
labeled as TD1 or TD2.
For
example, the deblurring result of the method ASDS_AR_NL_TD1 on image Parrot is labeled as
¡°ASDS_AR_NL_TD1_parrot¡±. Other result images are labeled similarly.
Experiment 1: 9¡Á9 uniform blur kernel, noise level ![]()
|
The
deblurring results on Barbara |
|
|
The
deblurring results on Bike |
|
|
The deblurring results on Straw |
|
|
The deblurring results on Boats |
|
|
The deblurring results on Parrots |
|
|
The deblurring results on Baboon |
|
|
The deblurring results on Hat |
|
|
The deblurring results on Pentagon |
|
|
The deblurring results on Cameraman |
|
|
The
deblurring results on Peppers |
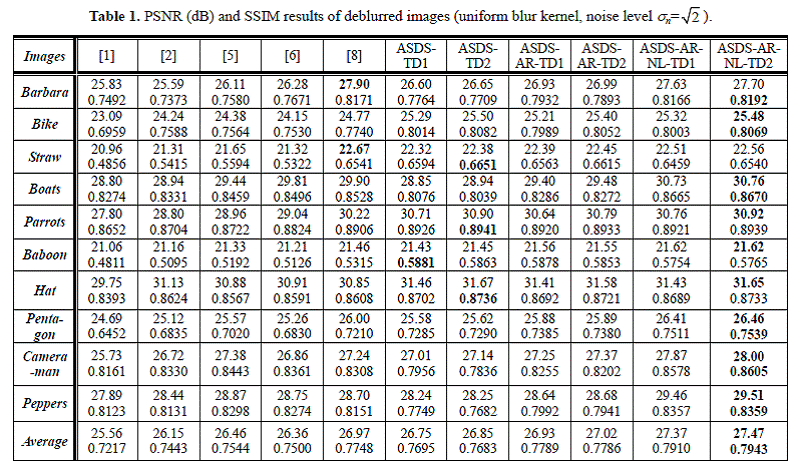
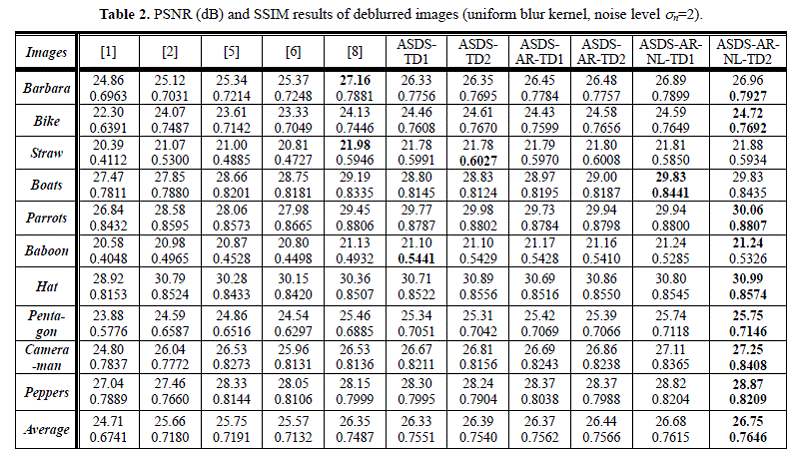
Experiment 2: 9¡Á9
uniform blur kernel, noise level ![]()
|
The
deblurring results on Barbara |
|
|
The
deblurring results on Bike |
|
|
The deblurring results on Straw |
|
|
The deblurring results on Boats |
|
|
The deblurring results on Parrots |
|
|
The deblurring results on Baboon |
|
|
The deblurring results on Hat |
|
|
The deblurring results on Pentagon |
|
|
The deblurring results on Cameraman |
|
|
The
deblurring results on Peppers |
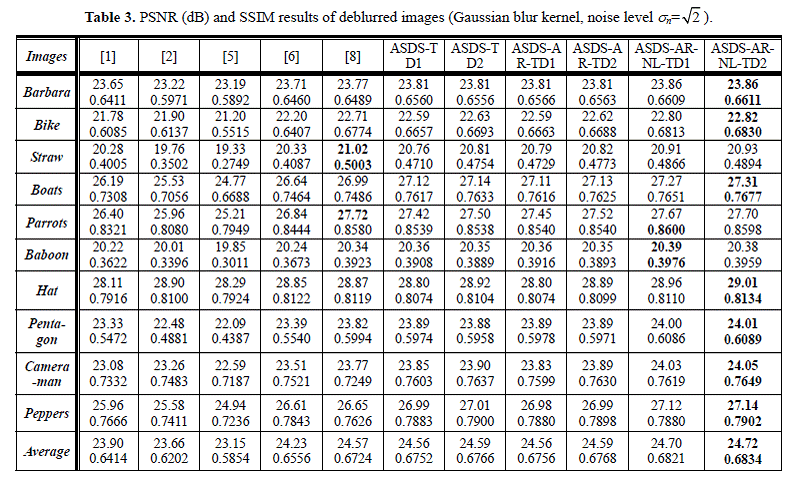
Experiment 3: Gaussian blur kernel with standard deviation 3, noise
level ![]()
|
The
deblurring results on Barbara |
|
|
The
deblurring results on Bike |
|
|
The deblurring results on Straw |
|
|
The deblurring results on Boats |
|
|
The deblurring results on Parrots |
|
|
The deblurring results on Baboon |
|
|
The deblurring results on Hat |
|
|
The deblurring results on Pentagon |
|
|
The deblurring results on Cameraman |
|
|
The
deblurring results on Peppers |
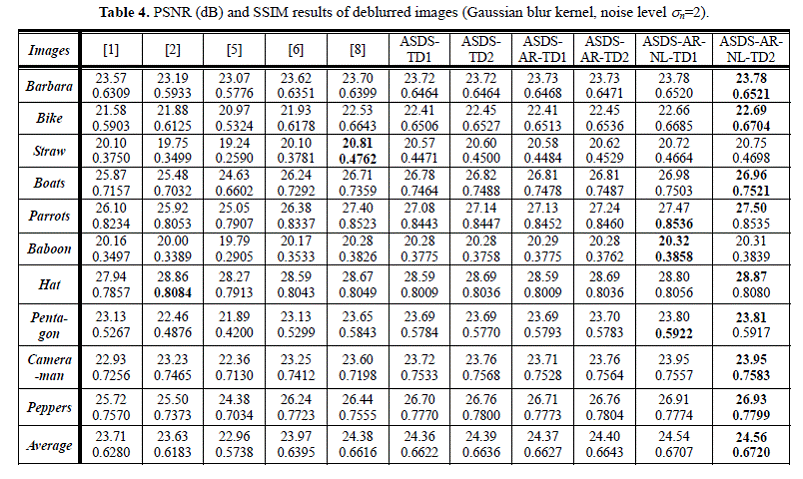
Experiment 4: Gaussian
blur kernel with standard deviation 3, noise level ![]()
|
The
deblurring results on Barbara |
|
|
The
deblurring results on Bike |
|
|
The deblurring results on Straw |
|
|
The deblurring results on Boats |
|
|
The deblurring results on Parrots |
|
|
The deblurring results on Baboon |
|
|
The deblurring results on Hat |
|
|
The deblurring results on Pentagon |
|
|
The deblurring results on Cameraman |
|
|
The
deblurring results on Peppers |
Part B: Results on Image Super-resolution
Notes:
(1)
The
super-resolution method in [1] is labeled as ¡°Surrogate¡±;
(2)
The
super-resolution method in [3] is labeled as ¡°Softcuts¡±;
(3)
The
super-resolution method in [4] is labeled as ¡°Sparse¡±;
(4)
The
super-resolution method in [7] is labeled as ¡°TV¡±;
(5)
The
proposed method by using only ASDS is
labeled as ASDS, by using ASDS plus AR
regularization is labeled as
ASDS-AR, by using ASDS with both AR and non-local regularization is
labeled as ASDS-AR-NL.
(6)
The
proposed deblurring method with training image dataset 1 or dataset 2 is
labeled as TD1 or TD2.
For example, the reconstructed high resolution image by the method ASDS_AR_NL_TD1 on image Girl is labeled as ¡°ASDS_AR_NL_TD1_girl¡±. Other result images are labeled similarly.
In Experiment 1 of
super-resolution, the degraded low resolution (LR) images were generated by
first applying a truncated 7´7 Gaussian smoothing filter with standard deviation 1.6 to the original
image and then down-sampling with a factor of 3.
In Experiment 2, Gaussian
white noise with standard deviation 5 was then added to the LR images to
simulate the noisy LR images.
Experiment 1: noiseless
images
|
The
supper-resolution results on Girl |
|
|
The
supper-resolution results on Parrot |
|
|
The supper-resolution results on Butterfly |
|
|
The supper-resolution results on Leaves |
|
|
The supper-resolution results on Parthenon |
|
|
The supper-resolution results on Flower |
|
|
The supper-resolution results on Hat |
|
|
The supper-resolution results on Racoon |
|
|
The supper-resolution results on Bike |
|
|
The
supper-resolution results on Plant |
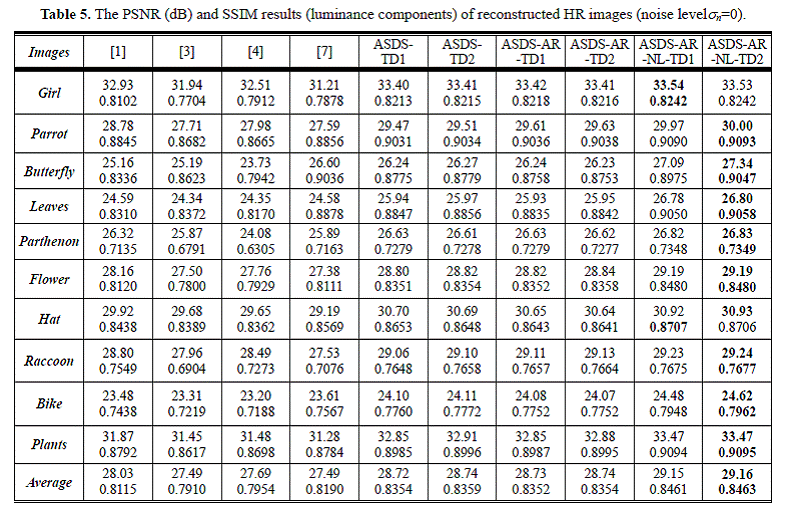
Experiment 2: noisy
images
|
The
supper-resolution results on Girl |
|
|
The
supper-resolution results on Parrot |
|
|
The supper-resolution results on Butterfly |
|
|
The supper-resolution results on Leaves |
|
|
The supper-resolution results on Parthenon |
|
|
The supper-resolution results on Flower |
|
|
The supper-resolution results on Hat |
|
|
The supper-resolution results on Racoon |
|
|
The supper-resolution results on Bike |
|
|
The
supper-resolution results on Plant |
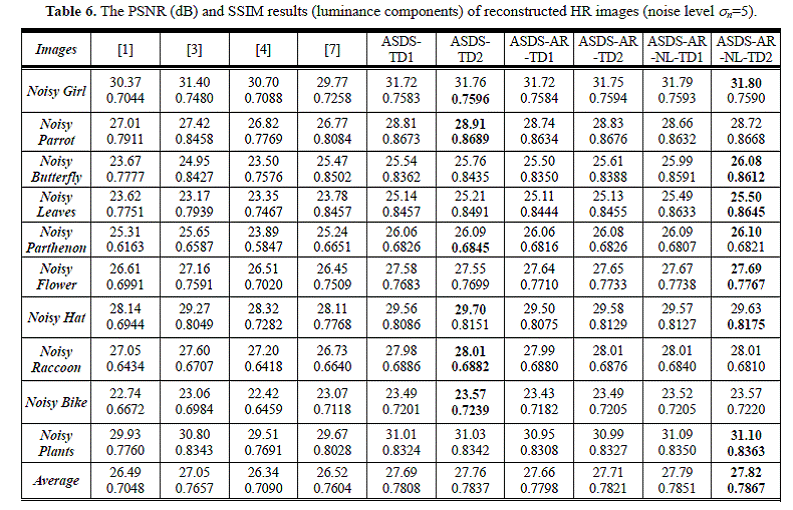
Part C: Results on the 1000-Image Dataset
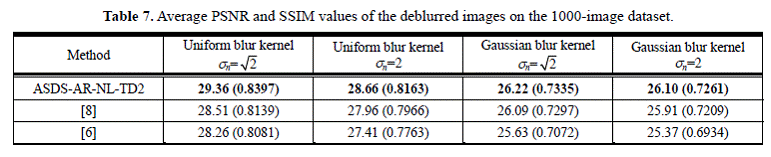
To more
comprehensively test the robustness of the proposed image restoration method, we
performed extensive deblurring and super-resolution experiments on a large
dataset that contains 1000 natural images of various contents. To establish
this dataset, we randomly downloaded 822 high-quality natural images from the Flickr website (http://www.flickr.com/),
and selected 178 high-quality natural images from the
Berkeley Segmentation Database (http://www.eecs.berkeley.edu/Research/Projects/CS/vision/grouping/segbench). A 256´256 sub-image that is rich in edge and
texture structures was cropped from each of these 1000 images to test our
method.
Results
on Deblurring
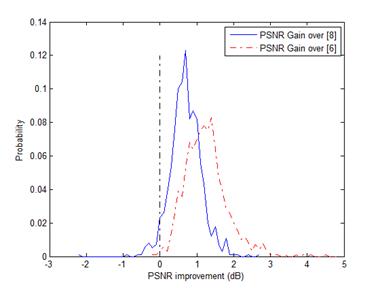
(a)
(b)
(c)
(d)
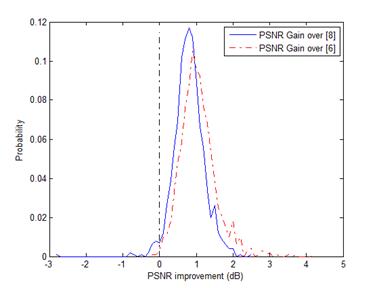
Fig. 1. The PSNR gain
distributions of deblurring experiments. (a) Uniform blur kernel with sn=1.414;
(b) Uniform blur kernel with sn=2; (c)
Gaussian blur kernel with sn=1.414;
(d) Gaussian blur kernel with sn=2.
Results
on Superresolution
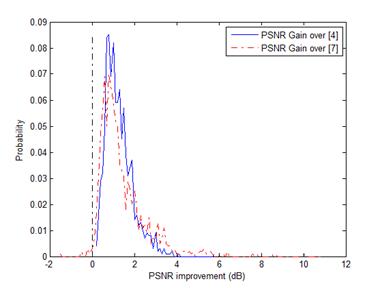
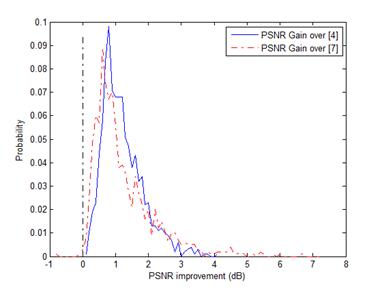
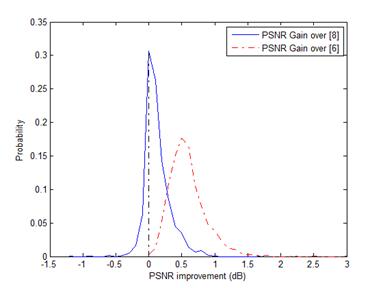
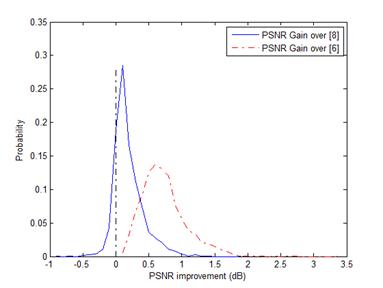
(a)
(b)
Fig. 2. The PSNR gain distributions of super-resolution experiments. (a)
Noise level sn=0; (b) Noise level sn=5.
References
[1].
Daubechies,
M. Defriese, and C. DeMol, ¡°An iterative thresholding algorithm for linear
inverse problems with a sparsity constraint,¡± Commun. Pure Appl. Math., Vol.57,
pp.1413-1457, 2004.
[2].
A. Beck and M.
Teboulle, ¡°Fast gradient-based algorithms for constrained total variation image
denoising and deblurring problems,¡± IEEE Trans. On Image Process., vol. 18, no.
11, pp. 2419-2434, Nov. 2009.
[3].
S.
Dai, M. Han, W. Xu, Y. Wu, Y. Gong, and A. K. Katsaggelos, ¡°SoftCuts: a soft
edge smoothness prior for color image super-resolution,¡± IEEE Trans. Image
Process., vol. 18, no. 5, pp. 969-981, May 2009.
[4].
J.
Yang, J. Wright, Y. Ma, and T. Huang, ¡°Image super-resolution as sparse
representation of raw image patches,¡± IEEE Computer Vision and Pattern
Recognition, Jun. 2008.
[5].
G.
Chantas, N. P. Galatsanos, R. Molina, A. K. Katsaggelos, ¡°Variational Bayesian
image restoration with a product of spatially weighted total variation image
priors,¡± IEEE Trans. Image Process., vol. 19, no. 2, pp. 351-362, Feb. 2010.
[6].
J.
Portilla, ¡°Image restoration through L
[7].
A. Marquina, and S.
J. Osher, ¡°Image super-resolution by TV-regularization and Bregman iteration,¡±
J. Sci. Comput., vol. 37, pp. 367-382, 2008.
[8].
K.
Dabov, A. Foi, V. Katkovnik, and K. Egiazarian, Image restoration by sparse 3D
transform-domain collaborative filtering,¡±in Society of Photo-Optical
Instrumentation Engineers (SPIE) Conference Series, vol. 6812, 2008.